Uzbekistan
UDC 539.3
CSCSTI 68.31
Russian Classification of Professions by Education 35.00.00
Russian Library and Bibliographic Classification 40
BISAC TEC003000 Agriculture / General
This article presents materials on the creation of a model of water intakes in a semi-limited reservoir in order to study the regularities of failures of an open collector-drainage network, as well as the impact of a decrease in their performance on the reclamation state of irrigated lands, taking into account the regulation of the reclamation regime of the soils of the Shuruzyak collector in the Syrdarya region. The authors consider a single well and a group of interacting wells located in any way, as well as a linear row of wells, of a very significant length near the Shuruzyak collector. The performed calculation shows an estimate of the balance with the identification of individual constituent sources, which ensure the flow rate of wells, which is most reliably produced by constructing filtration grids (graphically or based on modeling) using the method of adding currents. When calculating onshore water intakes in all the considered schemes, including those where the water intake is provided entirely by the inflow of groundwater from the coastline, the effect of an open collector must be taken into account. A decrease in the level under the action of pumping out of wells in such conditions should theoretically occur at all points of the formation, not only in the “capture zone”, limited by the neutral streamline, but also outside it, up to the collector.
open collector, borehole, onshore intakes, groundwater recharge, reservoir thickness, water loss, heterogeneous aquifers, permeability, d'Alembert-Euler ratio, semi-confined aquifer, split or "neutral" streamline
Введение. В связи со сложными природно-климатическими условиями во многих регионах страны, развитие сельского хозяйства без мелиорации не возможно. За последние пятнадцать лет более 80% прироста продукции растениеводства в стране получено за счет производства ее на мелиоративных землях.
Поддержание в работоспособном состоянии мелиоративных систем и сооружений требует огромных материальных, людских, временных и денежных затрат. Поддержание требуемой работоспособности открытой коллекторно-дренажной сети является основным условием обеспечения дренированности земель, как на системах горизонтального дренажа, так и при совместной работе горизонтального и вертикального дренажа.
В современных условиях на практике, в действующих нормативных документах и научных проработках ремонтно-восстановительные работы на системах открытого горизонтального дренажа планируется без увязки с показателями мелиоративного состояния земель, фактических мелиоративных режимов, показателей эксплуатационной надёжности открытых коллекторов, природно-хозяйственных и метеорологических условий.
В условиях экономической реформы возрастает значение научного обоснования сроков проведения ремонтно-восстановительных работ и их объемов учитывающих: влияние работоспособности открытых коллекторов на мелиоративное состояние земель, требование к поддержанию уровня дренированности, обеспечивающей регулирование мелиоративных режимов почв в оптимальных пределах.
Материалы и методы исследования. Исследования закономерности снижения работоспособности КДС с учетом водозаборов в полуограниченном пласте выполнены на основании анализа материалов и содержащихся в службах эксплуатации, проектных проработках и литературных источниках, путем систематизации и обобщения. При этом были использованы методы математической статистики и теории вероятностей.
Эмпирическое распределение случайной величины представляется либо в табличной форме, либо графически. Однако, необходимо знать цифровую характеристику распределения в более сжатой, компактной форме. Таких характеристик математическая статистика используются два вида:
- Положения центра рассеивания. Под центром рассеивания понимается тот интервал значений случайной величины, в котором она повторяется с наибольшей частотой. Иными словами, это некоторое среднее значение случайной величины, вокруг которых происходит более или менее плотное ее группирование.
- Характеристика рассеивания (мера колеблимости) случайной величины. Рассеивание характеризует несколько разбросана случайная величина около центра группирования. Оба вида характеристик называются статистическими мерами.
Результаты и обсуждение исследования. При моделировании водозаборов в долинах значительной ширины или «полуограниченном пласте», расчеты водозаборов производятся по формулам, которые легко составляются для одной или первой фазы фильтруемой многофазной жидкости, пользуясь методом многофазных жидкости и сложения фильтрационных течений. Эти формулы получены как предельные, при рассмотрении методики расчета водозаборов в полуограниченных водоносных пластах с учетом частичного их осушения в области выхода на поверхность [1].
Представляются эти водозаборы в следующем виде (рисунок 1-а).
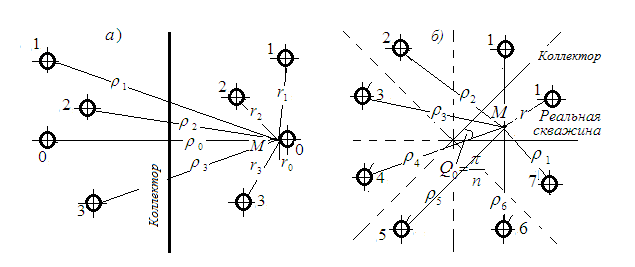
Рисунок 1 – Схемы к расчету скважин вблизи открытого коллектора в долинах весьма значительных поперечных размеров
а) берег русла открытого коллектора прямолинейный (полуограниченный пласт); б) берег русла схематически представляется в виде угла (пласт-угол)
Для одиночной скважины:
|
S = Q0 [Ei (-a0) - E (-a`)/ 4 πkm] |
(1) |
или для группы любым образом расположенных взаимодействующих скважин:
|
S = Q0 [Ei (-a0) - E (-a`)/ 4 πkm]– Qсум / ∑2i[Ei (-ai) - E (-a`)] |
(2) |
В этих формулах
ai = ri2 / 4at , ai` = pi2 / 4at
где r — расстояние точки, в которой определяется понижение уровня S , до реальной скважины;
p — то же до зеркального отображения скважины.
При определении понижения уровня в одной из скважин принимаются следующие обозначения:
r0— радиус скважины, в которой определяется понижение уровня;
p0— расстояние от этой скважины до ее зеркального отображения;
ri и pi - расстояния от той же скважины соответственно до всех взаимодействующих с ней реальных скважин и их зеркальных отображений;
и pi - расстояния от той же скважины соответственно до всех взаимодействующих с ней реальных скважин и их зеркальных отображений;
Q0, Qi (i=1,2,..., n) - расход каждой скважины,
Q сум = ∑Qi- суммарный расход всех скважин;
bi = Qi / Qсум
где i=1, 2,..., n  — число взаимодействующих скважин.
— число взаимодействующих скважин.
Значок показывает, что из суммы исключается скважина, в которой определяется понижение уровня.
При длительных откачках, когда pimax2 / 4at < 0,05...0,1, из зависимости (2) получаем хорошо известную формулу Форхгеймера для стационарных условий:
|
S = Q0/2πkm ln p0/r0 +Qсум / 4πkm ∑i=1n ln Bi ln p1/r1 |
(3) |
При откачке из одной скважины второй член в правой части уравнений (2) и (3) исключается, а при определении уровня в точке, удаленной от всех скважин, первый член выпадает. В связи с извилистостью береговой линии коллектора и наличием меандр нередко бывает целесообразно принимать в схеме контур пласта в виде некоторого угла (рисунок 1-б). В этом случае, если считать угол равным
где п — целое положительное число (n= 1,2,3,...).
Тогда формула для расчета группы любым образом расположенных взаимодействующих скважин может быть выражена следующим образом:
|
S = Q0/4πkm E1 (-a) + Qсум / 4πkm ∑i=12n-1(-1)i Ei (-a`i) |
(4) |
Эта формула получается из решения, данного М.М.Гылыбовым [4]. При она становится идентичной формуле (1) (для одиночной скважины, т.е. без суммы в правой части), а при,, кроме реальной скважины следует учитывать три зеркальных отображения, что соответствует схеме «пласта-квадранта».
При длительных откачках вместо формулы (4) имеем:
|
S = Q0/2πkm ln p1p3 p 2n-1 / r0p2 p2n-2 |
(5) |
Линейный ряд скважин, весьма значительной протяженности. При большом числе скважин, расположенных параллельно открытого коллектора в удалении от него на расстоянии L, для расчета можно использовать зависимость, получающуюся при замене реального ряда скважин галереей с погонным расходом
q0 = Q сум / 2 l
где Q сум — суммарный расход скважин;
 l — полудлина галереи.
l — полудлина галереи.
При этом, используя известное решение из теории теплопроводности для бесконечной линейной системы постояннодействующих источников и применяя зеркальное отображение [1], получим:
|
S = Ql / 2kmσ √F0 [ierfc |1- x| / 2 √F0 – ier 1+x / 2 √F0 |
(6) |
При длительных откачках формула (6) принимает следующий вид:
|
S = Qx / 2kmσ |
(7) |
При определении понижения уровня непосредственно в скважинах ряда, а также в точках, отстоящих от ряда в глубь берега, при x≥L
|
S= QL / 2kmσ |
(8) |
Для определения понижения уровня в скважинах ряда к выражению (8) следует добавить величину дополнительного сопротивления, определяемого в зависимости от размеров скважин, степени их несовершенства и расстановки в пределах ряда. При этом получим:
|
S = Q / 2kmσ [πl / σ + ln σ/ πr0 + ƍ] |
(9) |
где ƍ - поправка на несовершенство скважины;
r0- радиус скважины.
Во всех приведенных здесь формулах: σ- половина расстояния между скважинами (σ=l/ (n-1),
σ- половина расстояния между скважинами (σ=l/ (n-1), l - половина длины ряда,
l - половина длины ряда,  n - общее число скважин).
n - общее число скважин).
|
|
|
|
Рисунок 2 - Схема расчета линейного ряда скважин вблизи открытого коллектора |
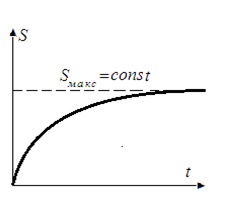
Рисунок 3 - График понижения уровня при откачке из скважин вблизи открытого коллектора |
При действии береговых водозаборов фильтрация со временем приобретает установившийся характер, кривая изменения уровня подземных вод в этих условиях довольно быстро выполаживается и становится параллельной оси абсцисс (рисунок 3). В соответствии с этим прогнозы на длительные эксплуатационные периоды практически следует производить по формулам (3), (5) и (7) - (9) для стационарного потока.
Задача о расчете бесконечных линейных рядов скважин в рассматриваемых условиях полуограниченного пласта в более строгой постановке исследовалась, Н.Н.Веригиным, В.С.Саркисяном, и Г.В.Насоновым [3]. Однако приближенные расчеты по формуле (6) - (8) при определении понижения уровня в скважинах дают практически одинаковый результат с расчетами по графикам и таблицам, в которых выражены решения указанных авторов.
При устройстве крупных водозаборов подземных вод в долинах с постояннодействующим речным стоком часто возникает вопрос о том, в какой мере эксплуатация таких водозаборов может отразиться на общем водном балансе коллектора.
При оценке суммарных ресурсов подземных вод в пределах крупных речных бассейнов необходимо учитывать, что изъятие подземных вод в размерах, обеспечиваемых инфильтрацией атмосферных осадков и поступлением воды из поверхностных источников, приведет к соответствующему уменьшению открытого водного стока. Однако при устройстве водозаборов на локальных участках влияние эксплуатации подземных вод на открытый водный сток должно оцениваться в зависимости от конкретных гидрогеологических и гидрологических условий, схемы размещения водозаборных сооружений, длительности их эксплуатации и т.д. [4].
Для выявления некоторых общих закономерностей рассмотрим простейшую схему фильтрации при откачке из скважины вблизи коллектора с учетом естественного берегового потока подземных вод.
Составим следующее уравнение:
S = Sскв + Se = Q/4πkm ·Ei (-r2 / 4at) +Ei (- p2/4at)+ qσ / km
где qσ - бытовой расход подземного потока
r2 = y2 +(x0-x)2
p2 = y2 + (x0+x)2
Составляющая скорости фильтрации по координате 
|
Vx = - k ð S / ðx = Q/ 2πm ·(x0-x /r2 ·e r2/4at + x0+x / p2 e p2/4at) – qσ/m |
(10) |
Здесь m- мощность пласта. При более или менее длительных откачках (когда p2 / 4at < 0.05//0.1) формируется квазистационарный режим фильтрации и можно принимать
|
Vx= Q/ 2πm ·(x0-x /r2 + x0+x / p2) - qσ/m |
(11) |
Приравнивая нулю это выражение, нетрудно получить координату точки разветвления потока, через которую проходит линия, ограничивающая область питания скважины. При этом можно представить себе такие случаи [2,3].
1. Расход скважины целиком обеспечивается фильтрацией из открытого коллектора (рисунок 4-а).
2. Расход скважины обеспечивается притоком подземных вод только со стороны берега (рисунок 4-б). Раздельная точка (максимум кривой депрессии) находится между скважиной и коллектором. Координаты раздельной точки:
|
xm = √x0(x0-Q/πq0) ; |
(12) |
3. Расход скважины обеспечивается береговым потоком, но раздельная точка смещается к коллектору (касается ее, рисунок 4-в).
|
ym =xm = 0, Q = πx0q0 |
(13) |
4. Расход скважины обеспечивается береговым потоком подземных вод и фильтрацией из открытого коллектора (рисунок 4-г). В данном случае образуются две раздельные точки, координаты которых:
xm = 0; ym = √ x0 (Q/ πq0 – x0) ; Q > x0q0 (14)
Через раздельную точку проходит так называемая раздельная или «нейтральная» линия тока, ограничивающая область питания скважины. Уравнение функции тока  легко получить из (11), используя известное соотношение Даламбера–Эйлера:
легко получить из (11), используя известное соотношение Даламбера–Эйлера:
|
ψ = - ʃvxdy = Q/ 2π [arctg ·y/x0-x + arctg ·y/x0+x ] – qσy +C |
(15) |
Полагая ψ=0 при X=0, получаем C=0. Тогда, задаваясь любым значением y и ψ=Q/2, можно из (15) найти координаты x раздельной линии тока.
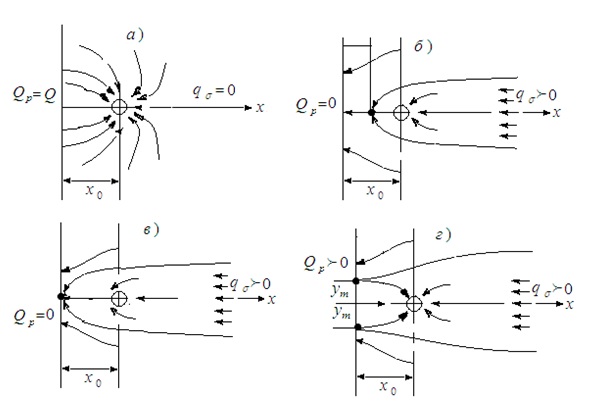
Рисунок 4 - Фильтрационные течения к скважине вблизи открытого коллектора
Величина расхода коллектора Qк определяется по тому же выражению (15):
Qk = 2mʃvx x=0 dy
Подставляя сюда значение vx по (10), получим интеграл:
В первой схеме, при q0= 0 (рисунок 4-а), теоретически фильтрация из открытого коллектора происходит на фронте бесконечно большой протяженности (ym=).
В этом случае следует, учитывать, что в реальных условиях фильтрация из коллектора может осуществляться лишь на ограниченных участках. Это связано с извилистостью русел, их заиленностью и частой сменой водопроницаемых русловых отложений водоупорными породами.
При длительных откачках, пользуясь в качестве исходной формулой (11), можно получить следующее выражение для расхода коллектора [2]:
|
Qk = 2Q/ π arctg ym/ x0 – 2q0ym |
(17) |
Здесь ym определяется по формуле (14). Ширина «зоны захвата» берегового потока B= 2ym находится из следующего балансового соотношения;
Qk=2Q/ π arctg ym/ x0 + 2 (B-ym)q0
Решая это последнее уравнение относительно В, получаем:
|
B=Q/πq0 arctg x0/ym + ym |
(18) |
|
Qk = Qerfc (1/2 √F0) |
(19) |
На примере расчета по формулам (14), (18) и (19) видно, что доля коллекторно-дренажных вод в общем расходе скважины может быть весьма существенной.
Таблица 1 – Результаты расчета Qk и B при некоторых значениях x0,Q,q0.
|
№ |
|
|
|
|
|
|
|
|
1. |
50 |
1000 |
0,2 |
279 |
981 |
786 |
78 |
|
2. |
50 |
1000 |
0,6 |
156 |
645 |
625 |
62 |
|
3. |
50 |
1000 |
1,0 |
117 |
494 |
518 |
51 |
|
4. |
200 |
826 |
0,2 |
472 |
1997 |
427 |
52 |
|
5. |
200 |
826 |
0,6 |
218 |
1071 |
184 |
22 |
|
6. |
200 |
826 |
1,0 |
112 |
722 |
8 |
10 |
При откачке из группы взаимодействующих скважин, любым образом расположенных вблизи открытого коллектора, оценку баланса с выявлением отдельных составляющих источников, которыми обеспечивается расход скважин, наиболее надежно можно производить путем построения фильтрационных сеток (графически или на основе моделирования) с использованием метода сложения течений.
Однако при небольшой длительности откачек (и значительных расстояниях скважины от открытого коллектора) результаты расчетов по приведенным формулам (1) и (3) оказываются практически близкими к результатам, получаемым по формулам для неограниченного пласта. Продолжительность этого периода находится по следующему соотношению [2]:
находится по следующему соотношению [2]:
|
tk<λρ2/a |
(20) |
Здесь λ = f (r2/4at) определяется по графику, изображенному на рисунке 5.
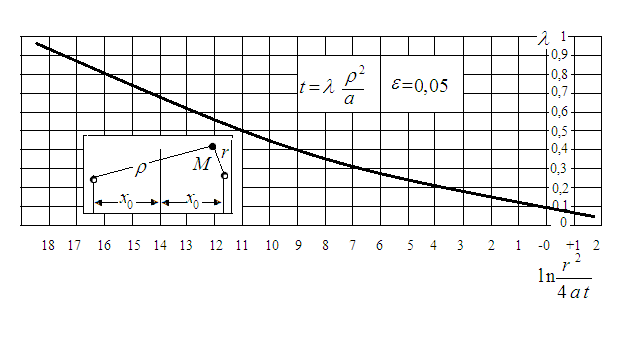
Рисунок 5 – График
Выводы. При моделировании водозаборов в полуограниченном пласте в целях управления мелиоративным режимом окрестности открытого коллектора, а также расчетах береговых водозаборов во всех рассмотренных схемах, в том числе в тех, где расход водозабора обеспечивается целиком притоком подземных вод со стороны береговой линии, необходимо учитывать влияние открытого коллектора. Понижение уровня под действием откачки из скважин в таких условиях теоретически должно происходить во всех точках пласта, не только в «зоне захвата», ограничивающейся нейтральной линией тока, но и за ее пределами вплоть до коллектора (хотя фильтрации из последней и не возникает).
1. Bochever F.M. Gidrogeologicheskie raschety krupnyh vodozaborov pod-zemnyh vod i vodoponizitel'nyh ustanovok. Stroyizdat, 1963.
2. Verigin N.N. O techeniyah gruntovyh vod pri mestnoy usilennoy in-fil'tracii. DAN SSSR, t. 20, № 5, 1950.
3. Verigin N.N., Sarkisyan V. S. Metod rascheta podzemnyh vodo¬zaborov i vertikal'nogo drenazha v poluogranichennoom vodonosnom plaste. Tr. VODGEO, vyp. 13, Gidrogeologiya. Gosstroyizdat, 1966.
4. Khudaykulov S. I., Yakhshibaev D. S., Usmonov A. H., Nishonov F.Kh. Shange in concentration of collector watersalong the flow length taking into account the difference in densities http://dx.doi.org/10.26739/2433-202x Issue DOI https://journalofresearch.asia/wp-content/uploads/2019/06/39-43.pdf Asian Journal of Research ¹ 1-3, 2019 ISSN 2433-202x IMPACT FACTOR JOURNAL DOIhttps://doi.org/10.26739/2433-202x SJIF 5,1 www.journalofresearch.asia IFS 2,7 info@journalofresearch.asia 39-43 p.
5. Argus ONE for All Ground Water Models. Version 4.0 // Environmental Sortware & Publications. Catalog 1997-1998. Washington, Scientific Software Group, 1998. - P. 6.
6. Cherepanskiy M.M. Issledovanie vzaimosvyazi poverhnostnyh i podzemnyh vod pri ih sovmestnoy ekspluatacii // PRIRODOPOL'ZOVANIE: Sb. nauch. / Pod red. I I. Lishtvana, V.F.Loginova. Mn.: IPIPRE HAH Belarusi, 2003. - Vyp.9. - S.81-89.
7. Isaev S.X., Radjabov T.T., Dolidudko A.I.- Influence of inorganic fertilizers on cotton crop yield in saline soils//Bulletin of Science and Practice. 2018, 4 No7, pp 160-165
8. Usmanov, R.N. O modelirovanii izmeneniy gidrogeohimicheskogo sostoyaniya gidrogeologicheskih ob'ektov na baze nechetko mnozhestvennogo podhoda // Uzb. zhurnal «Problemy informatiki i energetiki» - T. 2005. - № 6. - S. 67-72.
9. Siddaraju M.C., 1992. Digital Evaluation of aquifersof Suvernavathi river basis, Karnataka Unpub. Ph.D., thesis, Univ. of Mysore, 99 p.
10. Hantush M.S. Analysis of data from pumping wells near a river // Journal of Geophysical Research. 1959. - Vol. 64. - P. 1921-1932.