UDK 631.6 Сельскохозяйственная мелиорация
GRNTI 68.31 Сельскохозяйственная мелиорация
OKSO 35.06.01 Сельское хозяйство
BBK 4 СЕЛЬСКОЕ И ЛЕСНОЕ ХОЗЯЙСТВО. СЕЛЬСКОХОЗЯЙСТВЕННЫЕ И ЛЕСОХОЗЯЙСТВЕННЫЕ НАУКИ
TBK 56 Сельское хозяйство
BISAC TEC003000 Agriculture / General
Abstract. Modern drip irrigation systems are very expensive. In this regard, to improve the quality of their design, a mathematical model of fluid movement in drip lines and diluting pipelines was compiled, and a program in the Quick Basic programming language that implements an algorithm for solving the problem was developed. The developed mathematical model and the calculation program based on it allows obtaining graphs of the main hydraulic characteristics of the pipelines under consideration, conducting their comparative analysis and designing pipelines with optimal parameters.
Drip irrigation method, drip irrigation systems, fluid movement in cable lines and distribution pipelines, mathematical model, Euler differential equations and continuity, difference calculation method
Введение. Для выбора оптимальных длин и диаметров капельных линий, а также разводящих трубопроводов систем капельного орошения была разработана математическая модель движения жидкости в них и проведен вычислительный эксперимент
В системах капельного орошения капельницы располагаются по длине поливных трубопроводов или по длине капельных линий, которые берут начало из участковых или разводящих трубопроводов [4]. В связи с этим, движение жидкости в капельных линиях и разводящих трубопроводах установившееся с убывающей массой жидкости по длине [2]. Поэтому, математическая модель движения жидкости в этих трубопроводах состоит из уравнения Эйлера и уравнения неразрывности с учетом оттока массы жидкости по длине рассматриваемых трубопроводов ⦋1⦎.
где p – давление жидкости, Па;
𝑣 – скорость движения жидкости, м/с;
ρ – плотность жидкости,
ω – площадь живого сечения потока,
λ – коэффициент гидравлического трения;
d – диаметр трубопровода, м;
m – масса сосредоточенного оттока жидкости,
С учетом расхода оттока жидкости из трубопровода система уравнений (1) запишется в виде
где q – расход оттока жидкости из трубопровода,
Ɩ – длина трубопровода, на которой происходит отток жидкости, м.
Для решения дифференциальных уравнений математической модели применялся разностный метод. Узлы расчетных схем располагались вдоль оси рассматриваемых трубопроводов. Все производные, входящие в уравнения, были заменены конечными разностями. Из получившихся при этом алгебраических уравнений были получены расчетные уравнения, которые представлены системой уравнений (3).
Система уравнений (3) использовалась для расчета давления жидкости в узлах сетки, а скорости движения между узлами.
Для реализации разностного метода при решении дифференциальных уравнений необходимо использование вычислительной техники. Поэтому был разработан следующий алгоритм решения:
1. Ввод начальных и граничных условий.
2. Вычисление скорости движения жидкости по уравнению (2) системы уравнений (3).
3. Расчет числа Рейнольдса, определение области гидравлических сопротивлений.
4. Вычисление значения коэффициента гидравлического трения λ.
5. Расчет давления жидкости по уравнению (1) системы уравнений (3).
В соответствии с разработанным алгоритмом составлена программа расчета на языке программирования Quick Basic.
Состав исследований. Цель исследований заключалась в определении оптимальных диаметров и длин поливных и участковых трубопроводов для различных сельскохозяйственных культур, орошаемых капельным способом полива[3,4].
Ниже приводятся результаты вычислительного эксперимента для схем посадки плодовых культур 3,5
0,8; 3,5 0,9; 3,5 1,0 м, при этом считается, что яблони размещаются на шпалере и принят расход капельниц 
= 1,6 л/час, а размещение капельниц 3,5 0,5 м. В вычислительном эксперименте рассматривались поливные трубопроводы диаметром 14, 16, 18 и 20 мм длиной по 150 м, участковые трубопроводы диаметром 75, 90 и 110 мм длиной по 300 м, а также телескопические участковые трубопроводы, состоящие из двух участков диаметром 110 и 90 мм длиной по 150 м, и диаметром 90 и 75 мм по 150 м каждый.
Обсуждение исследований. Результаты исследований поливных трубопроводов представлены в виде графиков, которые приведены на рисунках 1, 2 и 3.
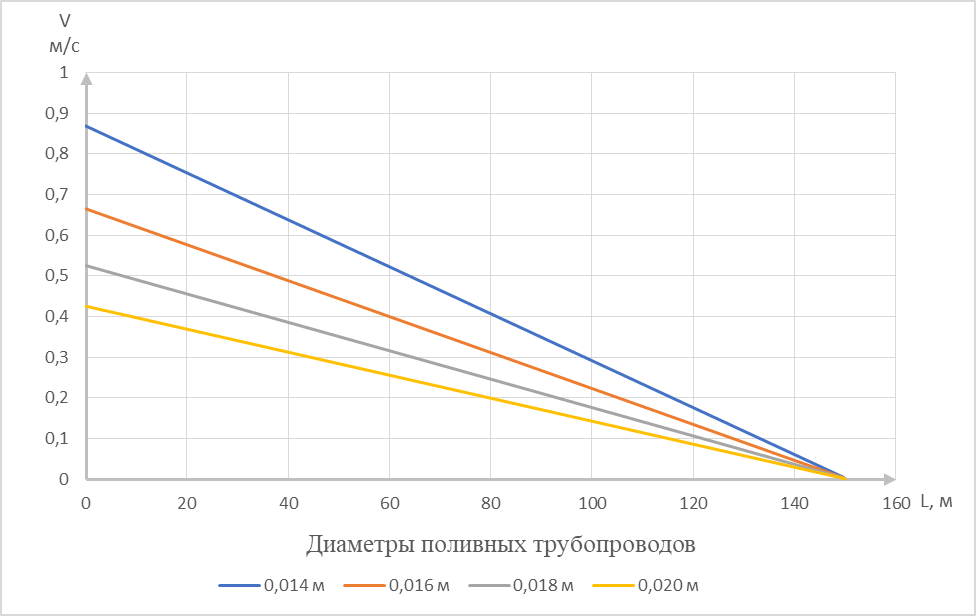
Рисунок 1 – Зависимость скорости движения жидкости от диаметра и длины капельных линий
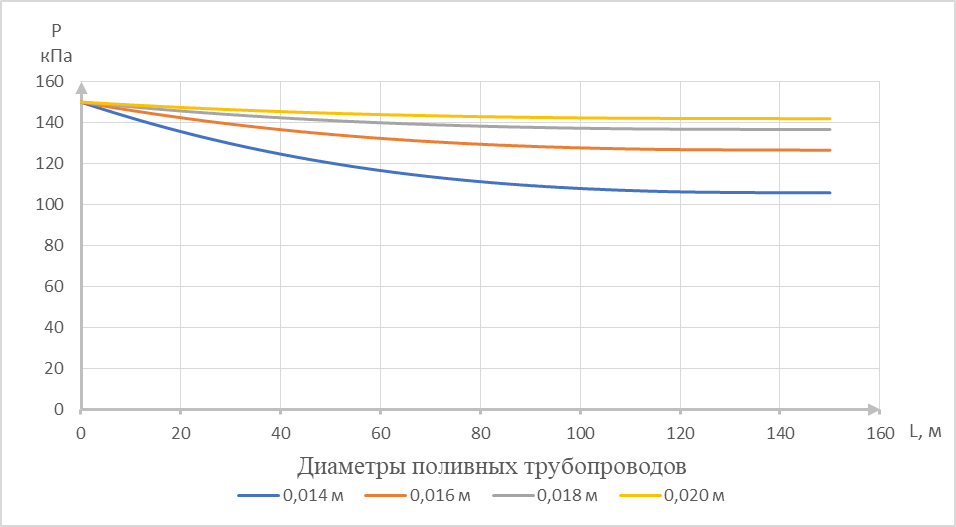
Рисунок 2 – Зависимость давления жидкости от диаметра и длины капельных линий
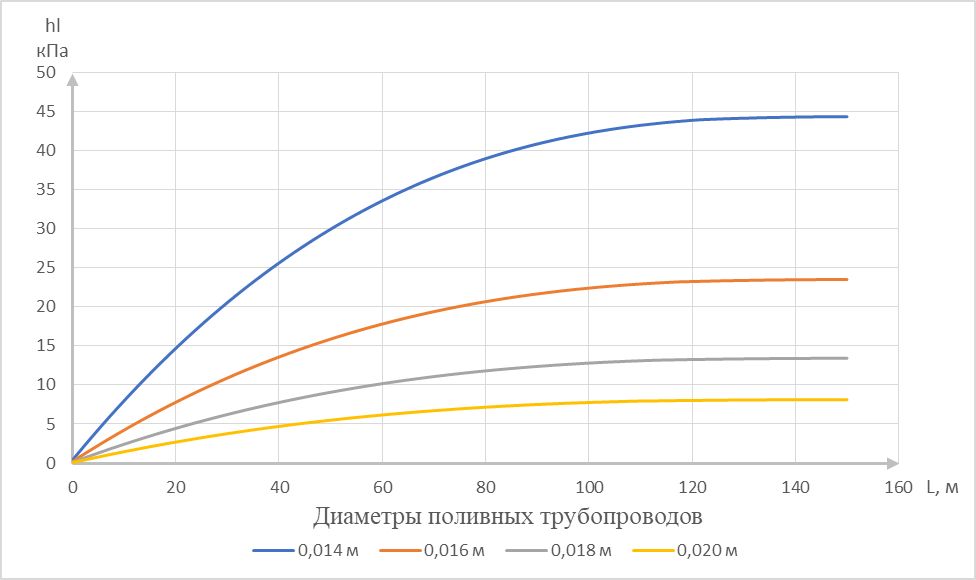
Рисунок 3 – Графики зависимости потерь напора от диаметра и длины капельных линий
На основании анализа полученных графиков, для орошения плодовых культур можно рекомендовать проектировать капельные линии длиной до 150 м и диаметром от 16 до 20 мм. Капельные линии диаметром 14 мм и меньше применять не рекомендуется, в связи с большими потерями напора.
Результаты исследований разводящих трубопроводов при схеме посадки деревьев 3,5
м и расходе капельниц 1,6 л/ч представлены на рисунках 4, 5 и 6.
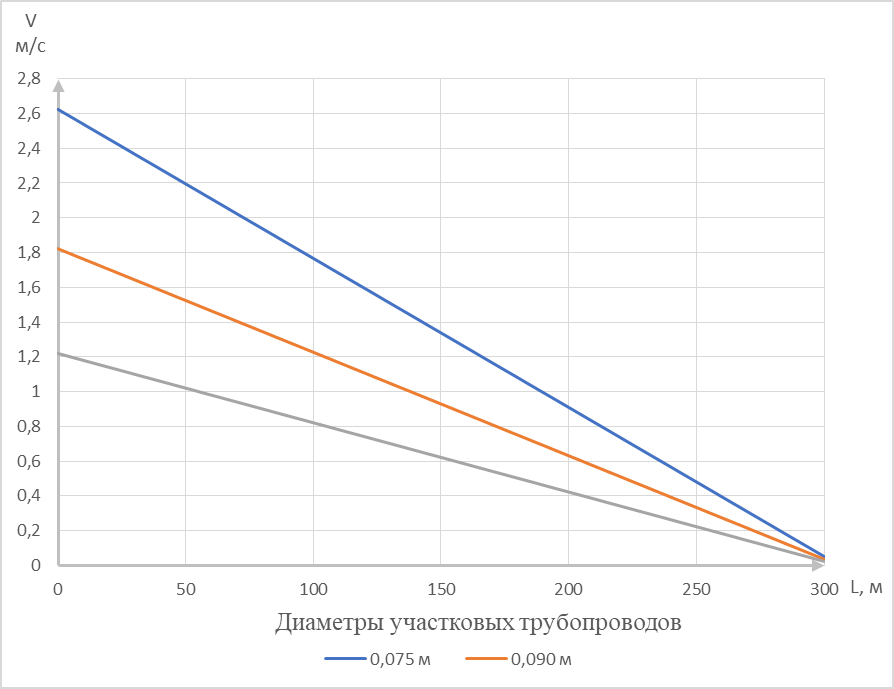
Рисунок 4 – Зависимость скорости движения жидкости от диаметра и длины разводящих трубопроводов
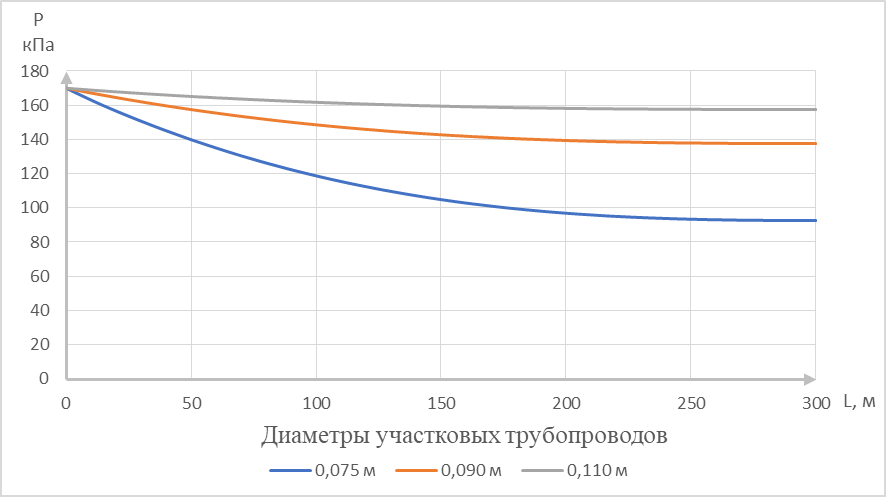
Рисунок 5 – Зависимость давления жидкости от диаметра и длины разводящих трубопроводов
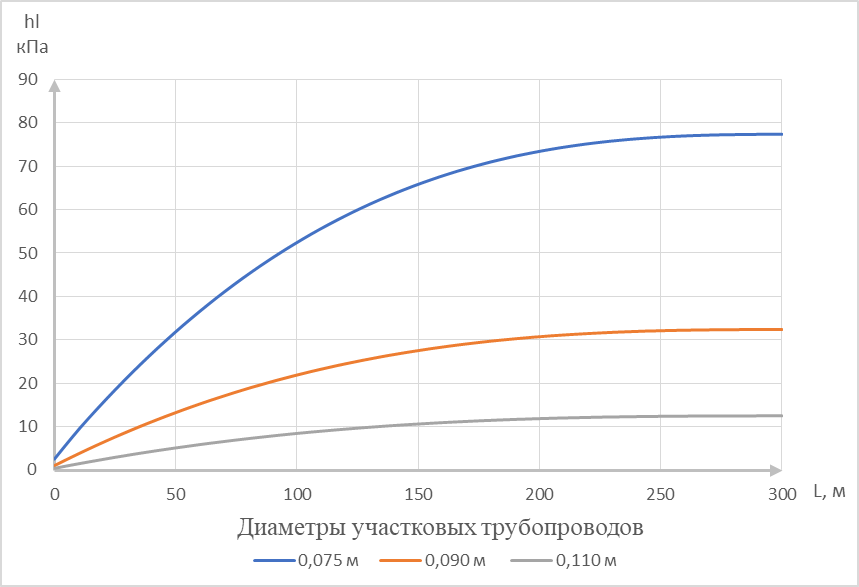
Рисунок 6 – Графики зависимости потерь напора от диаметра и длины разводящих трубопроводов
На основании анализа полученных графиков, для орошения плодовых культур можно рекомендовать проектировать участковые трубопроводы длиной до 300 м, а диаметром от 90 до 110 мм. Участковые трубопроводы диаметром 75 мм и меньше проектировать не рекомендуется, в связи с большими потерями напора.
Результаты исследований телескопических разводящих трубопроводов представлены на рисунках 7, 8 и 9.
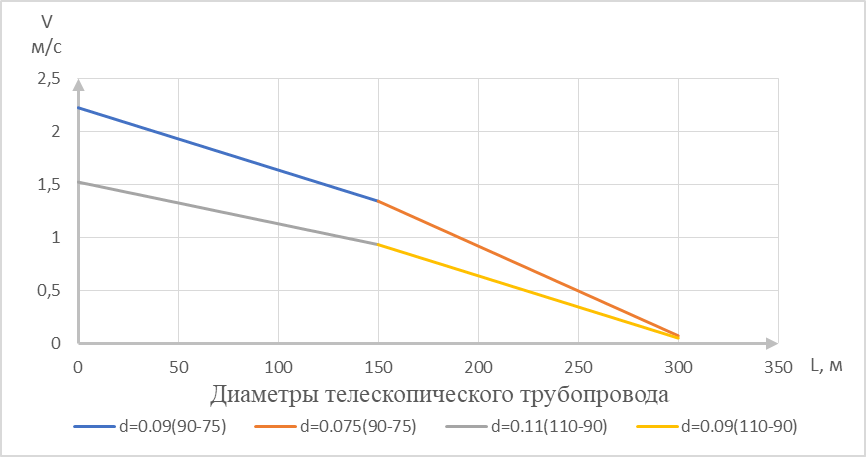
Рисунок 7 – Зависимость скорости движения жидкости от диаметров и длины телескопических разводящих трубопроводов
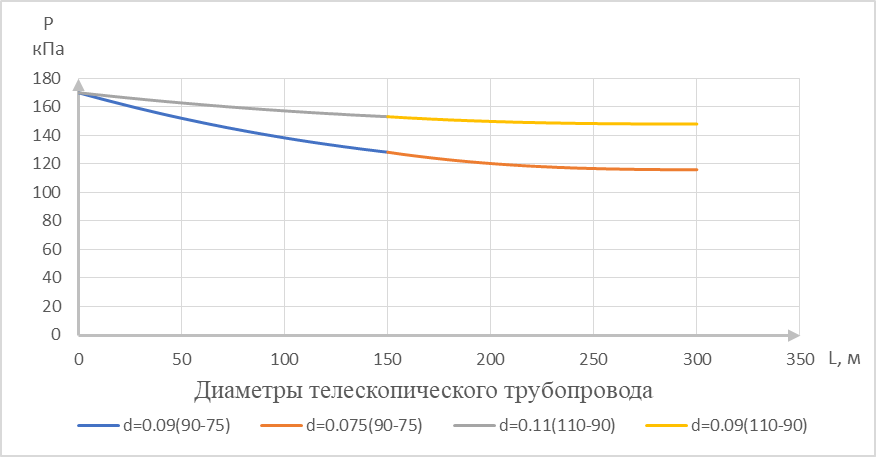
Рисунок 8 – Зависимость давления жидкости от диаметров и длины телескопических разводящих трубопроводов
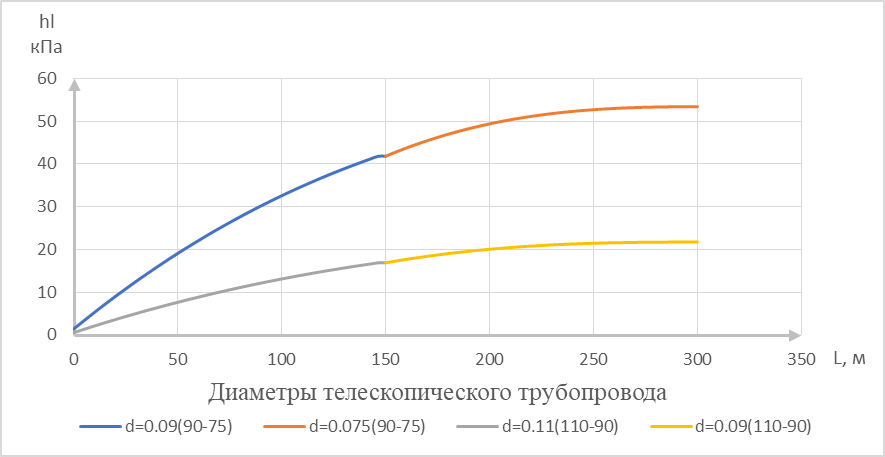
Рисунок 9 – Графики зависимости потерь напора от диаметров и длины телескопических разводящих трубопроводов
На основании анализа полученных графиков, для орошения плодовых культур можно рекомендовать проектировать телескопические участковые трубопроводы длиной до 300 м, диаметром 110 на 90 мм, состоящие из двух секций длиной по 150 м каждая. Телескопические трубопроводы длиной до 300 м, диаметром 90 на 75 мм применять не рекомендуется, в связи с большими потерями напора.
Результаты сравнительных исследований участковых трубопроводов постоянного диаметра и телескопических представлены на рисунке 10.
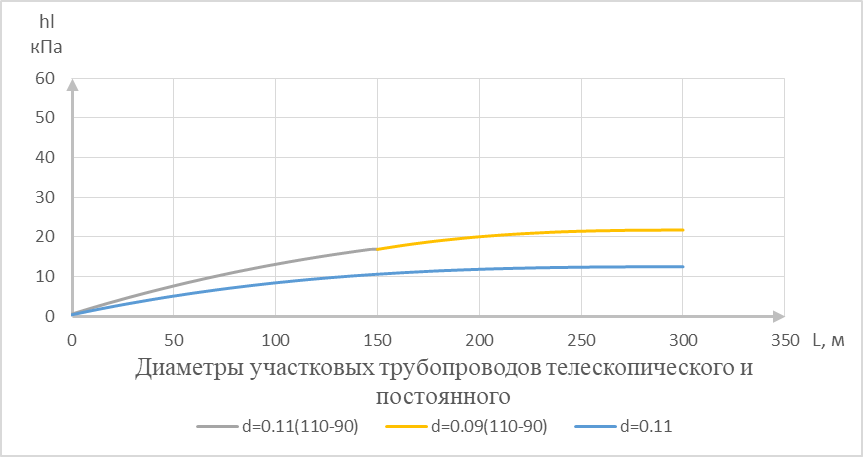
Рисунок 10 – Графики зависимости потерь напора от диаметра и длины телескопического разводящего трубопровода и разводящего трубопровода постоянного диаметра
Из рисунка следует, что потери напора в телескопическом разводящем трубопроводе несколько выше чем в разводящем трубопроводе постоянного диаметра, но увеличение потерь напора не значительное. В трубопроводе постоянного диаметра 1,15 м, а в телескопическом трубопроводе 2,1 м. Поэтому можно рекомендовать на системах капельного орошения применять и телескопические участковые трубопроводы, так как на фоне не значительного увеличения потерь напора можно получить экономию по стоимости трубопроводов.
Выводы. Современные системы капельного орошения являются весьма дорогостоящими, поэтому, в настоящее время значительно повышаются требования к качеству проектирования.
Разработанная математическая модель и составленная на ее основе программа расчета позволяет получать графики основных гидравлических характеристик рассматриваемых трубопроводов, проводить их сравнительный анализ и проектировать трубопроводы с оптимальными параметрами.
1. Ostrovsky N.V. Effective solutions for automation of localized irrigation systems / N. V. Ostrovsky, V. V. Vanzha, Yu. N. Samoylyukov, M. A. Bandurin, E. V. Degtyareva // Agrarian Scientific Journal.2021. 11. P. 102-107. DOI:https://doi.org/10.28983/asj.y2021i11pp102-107 EDN: XSKENO
2. Semerdzhjan A.K., Bukhanif I. Innovative types of irrigation of agricultural crops. In the book: The Year of Science and Technology 2021. Collection of abstracts based on the materials of the All-Russian Scientific and Practical Conference. The editor A.G. Koshchaev. Krasnodar, 2021. p. 271. EDN: QPZMYN
3. Semerdzhjan A.K. Improving the efficiency of providing irrigation water to systems located below the Krasnodar water reservoir / A.K. Semerdzhjan, V.V. Vanzha, V.I. Orekhova, E.V. Degtyareva // Land reclamation and water management. - 2022. - № 4. - P. 29-31. DOI:https://doi.org/10.32962/0235-2524-2022-4-29-31 EDN: YZBONA
4. Semerdzhjan A.K., Ben A.V. Experience in designing and construction of drip irrigation systems in Krasnodar Territory. In the proceedings: Results of the research work for 2017. Proceedings of the materials of the 73rd scientific and practical conference of teachers. 2018. P. 221-222. EDN: YWHNQL
