УДК 63 Сельское хозяйство. Лесное хозяйство. Охота. Рыбное хозяйство
ГРНТИ 68.31 Сельскохозяйственная мелиорация
ОКСО 110000 СЕЛЬСКОЕ И РЫБНОЕ ХОЗЯЙСТВО
ББК 40 Естественнонаучные и технические основы сельского хозяйства
BISAC TEC003000 Agriculture / General
При цифровизации результатов исследований вместо подбора эмпирических уравнений произвольной структуры предлагается использовать математическое моделирование на основе физического принципа баланса причинно-следственных взаимодействий в замкнутой физической системе. Раскрывается сущность данного принципа и приводятся примеры его применения при выводе «закона Дарси», формулы С.Ф. Аверьянова, связывающей влагопроводность почвогрунта с коэффициентом фильтрации, при обосновании структуры математической модели урожая сельскохозяйственных культур
математическое моделирование, коэффициент фильтрации, влагопроводность почвы, модель урожая
Во многих областях научных знаний, включая мелиоративную науку, имеется множество задач, которые невозможно решить без привлечения эмпирического анализа. Теоретические разработки, основанные на известных фундаментальных законах природы, в мелиоративной науке, связанной с воздействием на изучаемые процессы природных неуправляемых факторов, достаточно трудоемки, а чаще и невозможны по причине сложности объектов исследований. В результате для описания полученных результатов часто привлекаются эмпирические уравнения произвольной структуры. Эмпирические формулы присутствуют в работах практически всех ученых-мелиораторов, например, А. Н. Костякова, С. Ф. Аверьянова и др. [1-4]. Пестрота и многообразие предлагаемых эмпирических зависимостей, количество которых прогрессивно возрастает, вступают в противоречие с традиционным стремлением к единообразию и порядку, свойственным научному процессу. Постепенно приходит понимание необходимости разработки единой методологии получения и анализа опытных данных.
Как первый шаг при планировании, организации, проведении исследований и обобщении полученного экспериментального материала в качестве объединяющей методологической основы была предложена математическая теория планирования эксперимента, базирующаяся на идеях теории вероятности и математической статистики [5]. Однако математический аппарат теории планирования эксперимента в научных исследованиях используется весьма редко. Это вполне объяснимо, поскольку основные положения теории планирования эксперимента справедливы при проведении только активного опыта, в котором могут присутствовать только управляемые переменные [5]. В науке, связанной с изучением воздействия на изучаемые процессы техногенных управляемых и природных неуправляемых факторов, использование математической теории планирования эксперимента весьма ограничено. Поэтому нет оснований игнорировать и отвергать вынужденную опору многих ученых на эмпирический анализ с полным произволом в использовании разного вида эмпирических формул для представления результатов исследований.
Вместе с тем существуют объективные причины, ограничивающие использование эмпирики в научной деятельности. Эмпирические формулы произвольной структуры сами по себе при любом коэффициенте детерминации не являются действительными моделями исследуемых процессов, поскольку не имеют физического смысла, а представляют собой лишь формальное математическое сглаживание данных конкретных экспериментов [6]. Результаты применения эмпирико-статистических методик обработки данных опыта всегда являются частным решением, которое весьма сложно распространить даже на подобные исследования, но выполненные в других условиях. Это лишь промежуточный этап численного анализа, позволяющий установить наличие количественных связей в исследуемом процессе и их погрешность (коэффициенты детерминации).
Концепция обработки данных эксперимента на основе физического принципа. Возникает закономерный вопрос, а возможно ли вообще предложить некую объединяющую методологию обработки данных эксперимента. На первый взгляд такой методологии не может быть в принципе. Природа настолько многообразна, что вместить ее процессы в форму, ограниченную рамками одного закона, невозможно. Вместе с тем, на наш взгляд, эту проблему можно решать, используя математическое моделирование на основе физического принципа, который справедлив для неопределенного количества взаимодействий в материальном мире. Назовем его физическим принципом баланса причинно-следственных взаимодействий в замкнутой физической системе. Формулируется он следующим образом:
1. Бесконечно малое изменение вектора Y под воздействием факторов Х, Z и др. пропорционально произведению показателя восприимчивости Y к действию каждого фактора на характеристику воздействия каждого из них.
2. Каждый из факторов (Х, Z и др.), действующих на Y, сообщает ему такое же изменение, как если бы других факторов не было».
Заметим, что данный физический принцип априори предполагает независимость друг от друга факторов, действующих на Y и учитываемых при моделировании.
Для исследуемых процессов на основе сформулированного выше принципа предлагается выстраивать эмпирическую математическую модель с использованием полученной в эксперименте статистической информации. Формально этот принцип можно представить в виде обобщающего математического выражения:
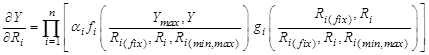
, (1)
где ∂Y/∂Ri – частная производная функции (Y) по i-му фактору (Ri), соответствующая интенсивности изменения Y при изменении Ri, при условии, что другие факторы (аргументы функции) не меняются; n – количество факторов (Х, Z и др.); αi – безразмерная константа, характеризующая изменение Y под воздействием i-го фактора; fi – функция, характеризующая восприимчивость Y по отношению к воздействию i-го фактора; Ri – обобщенное представление i-го фактора с его фиксированным значением (Ri(fix)), допустимыми минимумом (Ri(min)) или максимумом (Ri(max)); gi – функция, характеризующая управляющее воздействие i-го фактора на объект (Y). Вид функций fi и gi задается на основании данных опыта, которые формируют поле контролируемых переменных (Y, Ri).
Наиболее сложным и ответственным действием в предлагаемой нами схеме математического моделирования является установление вида исходных функций fi и gi. Укажем, что в первую очередь при этом требуется соблюдение следующих условий: необходимым условием является полное соответствие предлагаемых зависимостей физическим закономерностям, установленным в опытах; достаточное условие состоит в обязательном соблюдении баланса размерностей всех показателей, входящих в предлагаемые функции fi и gi. Поскольку эти функции задаются исследователем на основании закономерностей, установленных в опытах, то есть эмпирическим путем, конечное решение дифференциального уравнения (1) нельзя отнести к теоретическому результату. Но с полным основанием его можно считать полуэмпирическим.
Примеры применения принципа баланса причинно-следственных взаимодействий при построении экспериментальных математических моделей.
1. При внимательном анализе формулировки физического принципа баланса причинно-следственных взаимодействий в замкнутой физической системе находим его некоторое подобие так называемому «закону Дарси», широко используемому в мелиоративной науке. Применим выражение (1) для вывода данного закона, установленного ранее эмпирическим путем. Для этого сформулируем основные закономерности, установленные в опытах Дарси: 1) напор фильтрации (Н) и длина фильтрации (L) являются независящими друг от друга факторами, управляющими процессом фильтрации; 2) скорость фильтрации воды (V) через поровое пространство почвогрунта пропорциональна напору фильтрации (Н) и обратнопропорциональна длине пути фильтрации (L); 3) с увеличением или уменьшением градиента напора (отношения H/L) прямая пропорциональность скорости фильтрации градиенту напора нарушается, что объясняется увеличением роли поверхностных сил, наличием электрокинетических и осмотических эффектов, изменением характера фильтрационного потока от ламинарного к турбулентному [4].
Согласно установленным закономерностям можем предложить следующие эмпирические функции связи
![]() (2)
(2)
![]() , (3)
, (3)
где VH(fix) – фиксированная по координате Н скорость фильтрации, определяемая в заданной системе отсчета единичным напором Нfix , равным фиксированной длине пути фильтрации (Lfix), то есть при Hfix= Lfix = 1.
Согласно (2) и (3) соотношение (1) приводится к виду
![]() или
или .png) , (4)
, (4)
.png) (5)
(5)
где аH – безразмерная константа, характеризующая изменение скорости фильтрации при изменении напора. Зависит от геометрии порового пространства по координате Н (по вертикали).
Решением (4) является уравнение
Аналогичным образом обозначим функции fL и gL относительно длины пути фильтрации
.png) (6)
(6)
.png) (7)
(7)
где VL(fix) – фиксированная по координате L скорость фильтрации, соответствующая фиксированной в заданной системе отсчета единичной длине пути фильтрации (Lfix =1).
Знаком «минус» выражена обратная пропорциональность между длиной пути фильтрации и ее скоростью.
В соответствии с зависимостями (6) и (7) из соотношения (1) получаем
![]() или
или .png) , (8)
, (8)
где аL – безразмерная константа, характеризующая изменение скорости фильтрации при изменении длины пути фильтрации. Зависит от геометрии порового пространства по координате L (по горизонтали).
Решением (8) является уравнение
.png)
.
(9)
Поскольку каждый из факторов (Н, L), действующих на V, сообщает такое же изменение, как если бы других факторов не было, окончательным решением (1) будет произведение функций (5) и (9), то есть
.png) , (10)
, (10)
Выше указано, что Hfix = Lfix =1. Но при таком равенстве напора и длины пути фильтрации скорость фильтрации тождественна коэффициенту фильтрации (kф) [4]
VH, L(fix) = kф . (11)
С учетом (11) из (10) следует формула
![]() . (12)
. (12)
Таким образом, в результате несложного вывода из обобщенной функции (1) получено выражение закона Дарси, справедливое для любых условий. В простейшем случае αH = αL = 1. Но уравнивать между собой безразмерные константы αН и αL можно только в изотропном поровом пространстве.
2. Решим вторую задачу. С использованием принципа баланса причинно-следственных взаимодействий найдем зависимость коэффициента влагопроводности почвогрунта от его коэффициента фильтрации. Для этого сформулируем основные закономерности, установленные в опытах [2]: 1) коэффициент влагопроводности определяется содержанием влаги в почве сверх минимума, равного содержанию в почве связной влаги, не способной передвигаться под воздействием градиентов, действующих в наблюдаемых условиях; 2) при повышении насыщения почвы влагой до полной влагоемкости действующий на влагу градиент возрастает до единицы, при этом коэффициент влагопроводности сравнивается с коэффициентом фильтрации.
Выше назван только один фактор, влияющий на коэффициент влагопроводности, – содержание влаги в почве (влажность почвы). Поскольку искомая математическая модель, как и в первой задаче, представляет передвижение влаги в порах почвогрунта, обозначим по аналогии с (2) и (3)
.png) (13)
(13)
![]() (14)
(14)
где Wfix – фиксированная влажность почвогрунта в крайних границах его влагонасыщения, т.е. имеющая место при полном насыщении влагой (полная влагоемкость – WПВ) и при минимуме влагосодержания, определяемого связной влагой (W0).
Согласно (13) и (14) из (1) получим
![]() или
или .png) (15)
(15)
где аk – безразмерная константа, характеризующая изменение коэффициента влагопроводности при изменении влагонасыщения почвы. Зависит от геометрии порового пространства.
Решением (8) является уравнение
.png) или
или .png) . (16)
. (16)
Мы получили известную формулу С.Ф. Аверьянова [2]. Причем, как показывает алгоритм приведенного выше вывода, формулы Дарси (12) и Аверьянова (16) можно объединить в одну зависимость, характеризующую закономерности передвижения влаги в поровом пространстве почвогрунта при разных граничных условиях. Полученные формулы (12) и (16) предельно упрощены, но тем не менее, они являются работоспособными математическими моделями исследуемых процессов.
3. Рассмотрим задачу из совершенно другого направления исследований – разработка модели урожая сельскохозяйственных культур. Ранее нами было представлено довольно громоздкое ее решение [7]. Теперь выполним его на основе принципа баланса причинно-следственных взаимодействий, согласно которому бесконечно малое изменение урожая под воздействием урожаеформирующих факторов пропорционально произведению показателя восприимчивости урожая к действию каждого урожаеформирующего фактора на характеристику воздействия каждого их них.
Формально этот принцип для математической модели урожая повторяет выражение (1) в котором Ri является обобщенным представлением i-го урожаеформирующего фактора с его оптимумом (Ri(fix) = Ri(opt)), допустимыми минимумом (Ri(min)) или максимумом (Ri(max)). Вид функций fi и gi задается на основании данных опыта, которые формируют поле контролируемых переменных (Y, Ri). При этом учитываются установленные опытным путем закономерности [7-16]:
1) растения являются системой с памятью, то есть прирост урожая зависит от условий его формирования, определяемых факторами среды;
2) основные урожаеформирующие факторы (питание влага, тепло) равноценны и подобны по воздействию на растения, то есть не могут заменять друг друга и действуют по единообразной схеме (имеют минимум, оптимум, максимум);
3) если условия среды (влага, пища, тепло и др.) находятся в оптимуме, то растения образуют максимум урожая;
4) при отклонении фактора от оптимального значения в любую сторону (к минимуму или к максимуму) растения испытывают стресс, который снижает урожай;
5) величина отклонения фактических значений факторов среды (доз вносимых удобрений, влагообеспеченности культуры, температуры воздуха) от их оптимума определяет величину стресса, испытываемого растениями при формировании урожая;
6) с приближением условий среды к оптимуму прирост урожая замедляется;
7) наибольшее влияние на снижение урожая оказывает фактор, находящийся в минимуме.
Результаты анализа многочисленных данных [7-16] показывают, что в пределах 0,3Ri(opt)<Ri<1,7Ri(opt) математическое выражение принципа баланса причинно-следственных взаимодействий в системе «факторы среды (причина) – урожай (следствие)» можно представить в следующем виде:
- восприимчивость (проводимость) урожая к действию i-го фактора пропорциональна отношению величины урожая (по i-му фактору) к максимальной величине стресса от воздействия фактора, то есть
.png) , (17)
, (17)
где Y – урожай; Ri(opt) – оптимальное значение i-го фактора, при котором урожай достигает своего максимума; Ri(min, max) – минимальное или максимальное значение i-го фактора, при котором урожай не формируется;
- характеристика управляющего воздействия i-го фактора на урожай равна относительной величине стресса от воздействия данного фактора, который равен отношению стресса (недостатка до оптимума) к возможному его максимуму, то есть
![]() . (18)
. (18)
где Ri – фактическое значение i-го фактора среды.
С учетом зависимостей (17) и (18) решением дифференциального уравнения (1) является
.png) , (19)
, (19)
где Yn(max) – максимум урожая при учете n факторов; n – количество учитываемых факторов.
Анализ опытных данных показывает, что функцию fi (восприимчивость урожая к действию i-го фактора) в окрестностях Ymax можно свести к более простому соотношению
.png) , (20)
, (20)
Из (18) и (20) получим
.png)
(21)
Решения (19) и (21) являются вариантами эмпирической математической модели урожая, в которых каждая составляющая имеет конкретную физическую природу. Они идентичны формулам, полученным нами ранее с использованием данных полевых опытов, проведенных в Российской Федерации [7]. Дополнительно оценить точность (19) и (21) можно по результатам независимого эксперимента, в качестве которого нами использованы данные доктора сельскохозяйственных наук профессора Н. Н. Семененко, изучавшего влияние минерального питания на урожай ячменя и озимого тритикале, возделываемых на осушенных органогенных почвах Полесья [15]. Анализ показал, что экспоненциальная (19) и параболическая (21) зависимости приблизительно равноценны по точности, а ошибки вычислений по каждому варианту математической модели урожая зерновых культур превышают ошибки опыта (НСР05) не более, чем в 1,5 раза, то есть сравнимы с ними, колеблясь в пределах 5-9 % от фактического урожая [17].
Заключение.
Использование физического принципа баланса причинно-следственных взаимодействий в замкнутой физической системе позволяет решать разноплановые задачи путем построения эмпирических математических моделей исследуемых процессов с использованием полученной в экспериментах статистической информации. Применение данного принципа продемонстрировано при выводе «закона Дарси», формулы С.Ф. Аверьянова, связывающей влагопроводность почвогрунта с коэффициентом фильтрации, при обосновании структуры математической модели урожая сельскохозяйственных культур.
1. Костяков А. Н. Основы мелиораций. - М.: Сельхозгиз, 1960. - 622 с.
2. Аверьянов, С. Ф. Зависимость водопроницаемости почвогрунтов от содержания в них воздуха / С. Ф.Аверьянов // Доклады АН СССР. - 1949. - Т. 69, № 2 . - С. 141-144.
3. Аверьянов, С. Ф. Некоторые математические модели системы «растение-среда» / С. Ф.Аверьянов, В. В. Шабанов // Физическое и математическое моделирование в мелиорации. - М.: Колос. - 1973. - С. 293-295.
4. Мелиоративная энциклопедия. Сост. Б. С. Маслов. - М.: ФГНУ «Росинформагротех». - 2003. - Т. 1. - 670 с.
5. Красовский, Г. И., Филаретов, Г. Ф. Планирование эксперимента / Г. И. Красовский, Г. Ф. Филаретов. - Минск: Изд-во БГУ. - 1982. - 303 с.
6. Вахонин, Н. К. Моделирование урожаев в системе точного земледелия / Н. К. Вахонин // Мелиорация. - 2015. - № 1 (73). - С. 131-136.
7. Лихацевич, А. П. Использование обобщенной математической модели для анализа результатов многофакторных агрономических опытов // Мелиорация и водное хозяйство. - 2018. - № 2. С. 31-35.
8. Балакай, Г. Т. Научные основы возделывания сои на орошаемых землях Северного Кавказа. - Автореферат дисс. докт. с.-х. наук / Г. Т. Балакай. - Новочеркасск. - 2000. - 51 с.
9. Сухарев, В. И. Воднобалансовое и природоохранное обоснование мелиоративных мероприятий в агроландшафтах Центрально-Черноземного региона. - Автореферат дисс. докт. с.-х. наук / В. И. Сухарев. - Курск. - 2006. - 46 с.
10. Машарова О. В. Режим орошения и удобрения баклажанов при поливе дождеванием на светло-каштановых почвах Волго-Донского междуречья. - Автореферат дисс. канд. с.-х. наук / О. В. Машарова. - Волгоград. - 2011. - 24 с.
11. Богданенко, М. П. Технология возделывания рассадного лука при капельном орошении в Нижнем Поволжье. - Автореферат дисс. канд. с.-х. наук / М. П. Богданенко. - Саратов. - 2012. - 24 с.
12. Степуро, М. Ф. Использование методов математического моделирования при оптимизации систем удобрения моркови / М. Ф. Степуро // Картофель и овощи. - 2013. - №1. - С. 19-21.
13. Валге, А. М. Математическое моделирование урожайности многолетних трав / А. М. Валге, Э. А. Папушин, А. Н. Перекопский // Вестник Российской академии сельскохозяйственных наук. - 2013. - №5. - С. 8-10.
14. Шаповалов, Н. К. Математическое моделирование управления продукционным процессом на посевах сахарной свеклы / Н. К. Шаповалов, И. Е. Солдат // Достижения науки и техники АПК. - 2013. - №2. - С. 29-31.
15. Семененко, Н. Н. Торфяно-болотные почвы Полесья: трансформация и пути эффективного использования / Н. Н. Семененко. - Минск: Беларуская навука, 2015. - 282 с.
16. Топаж, А. Г. Абнормальные формы функции отклика «удобрения-продуктивность»: полевые наблюдения и модельный анализ / А. Г. Топаж, П. В. Лекомцев, А. В. Пасынков, А. В. Пуховский // Известия ТСХА. - Выпуск 2. - 2015. - С. 15-27.
17. Лихацевич, А. П. Математическая модель урожая сельскохозяйственных культур / А. П. Лихацевич. // Вес. Нац. акад. навук Беларусi. Сер. аграр. навук. - 2021. - Т. 59, №3. - С. 304-318.









