Приморский край, Россия
УДК 626.01 Научные основы гидротехнического строительства
ГРНТИ 68.31 Сельскохозяйственная мелиорация
ОКСО 35.00.00 Сельское, лесное и рыбное хозяйство
ББК 385 Строительные конструкции
BISAC TEC003000 Agriculture / General
В работе рассматривается применение вариационного принципа минимума кривизны в разработке нового метода профилирования быков водосливных сооружений. В результате исследования был получен новый теоретический метод расчета формы криволинейного заостренного быка с равным влиянием на пропускную способность, но имеющий меньшую площадь и, следовательно, меньшие затраты на строительные материалы и возведение конструкции. При анализе исходного метода расчета обнаружена ошибочность распространенного утверждения, что при равных граничных условиях наименьшие размеры имеет профиль, построенный по форме дуги окружности. Проведено компьютерное моделирование и выполнен анализ влияния формы оголовка опоры на пропускную способность сооружения.
водосливы, компьютерное моделирование, вариационный принцип, принцип минимума кривизны, ANSYS Fluent
Быки водосливов являются необходимым элементов крупных водосбросных гидротехнических сооружений. Они разбивают водосливной фронт водослива на отдельные секции, служат опорами для технологических мостов и местом установки затворов. К быкам предъявляются два основных требования – минимизация негативного влияния на пропускную способность сооружения и обеспечение беспрепятственного пропуска плавающих тел в нижний бьеф сооружения. Аналогичные требования и правила профилирования налагаются на опоры мостов. В большинстве случаев, очертания быков в плане выполняются круглыми или криволинейного заостренного очертания. Именно эффективность профилирования наибольшим образом определяет влияние на пропускную способность и расход строительных материалов.
В настоящее время самым распространенным методом профилирования быка является построение по форме дуги окружности. Оно основано на применении вариационного метода – решении классической изопериметрической задачи: «какая фигура будет иметь максимальную площадь при одинаковом периметре?». Подробное решение данной задачи на примере поиска оптимальной формы сечения канала представлено в работе [1] и даёт идентичные результаты. Противоречие заключено уже в исходной формулировке задачи, форма быка имеет максимально возможную площадь, при выполнении налагаемых граничных условий: плавного сопряжения быка с поверхностью опоры и реализации заданного угла обтекания.
Для построения быка с минимальными площадью и смоченным периметром, а также с соблюдением всех налагаемых граничных условий в исследовании использован вариационный принцип минимума кривизны.
Цель исследования – применить вариационный принцип минимума кривизны в профилировании быков водосливных и мостовых сооружений оптимальной конструкции.
Теоретическое исследование.
Вариационный принцип минимума кривизны приведен в интерпретации успешно примененной в работах [2] и [3]: «минимальную кривизну имеет прямая линия, следовательно, при стремлении потока реализовать движение с траекториями минимальной кривизны с допускаемыми связями любая кривая будет стремиться к прямой, в таком случае минимизировать следует разницу между выбранным полиноминальным уравнением и прямой линией». Применение прямого метода Ритца позволило получить безразмерное уравнение (1) линии минимальной кривизны, удовлетворяющей заданным граничным условиям [3]:
где: 
– её высота.
Данное уравнение использовалось при расчетах траектории струи при падении потока с горизонтальной площадки. В таких задачах величины – её высота, являются известными величинами. При проектировании быков водосливов, ширина быка определяется характеристиками мостов и затворов. Длина криволинейного заостренного оголовка быка является неизвестной и зависит от формообразующей линии и угла заострения оголовка быка. В рассматриваемой задаче величина
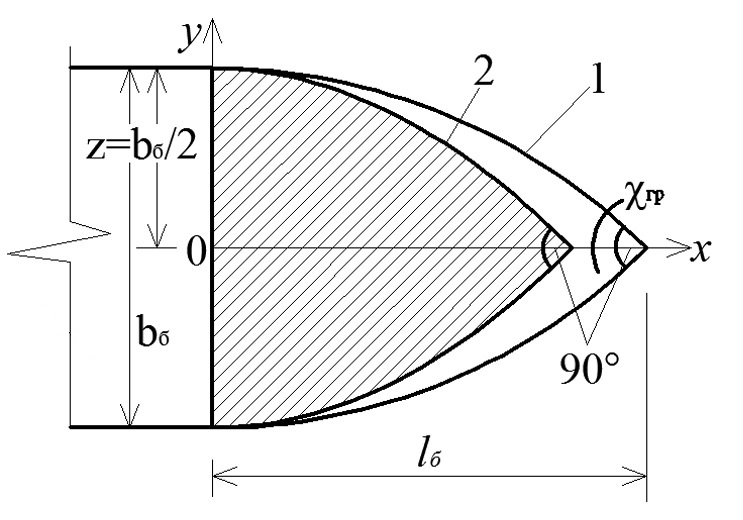
Рисунок 1. Схема водосливного быка, где: 1 – оголовок быка, построенный по форме дуги окружности, 2 – оголовок быка, построенный с использованием принципа минимума кривизны, 
– толщина быка, 
– длина криволинейного оголовка быка.
В задаче введено дополнительное граничное условие – наличие определенного полуугла заострения оголовка быка
Введем новое граничное условие:
при
Знак «-» является следствием наличия обратного уклона грани в системе координат и вследствие тригонометрического правила
Полученное уравнение позволяет избавиться от одной из двух неизвестных или . При этом ширина быка определяется шириной водосливного отверстия, воспринимаемой нагрузкой и габаритами установленного оборудования. Величина же зависит от требуемого угла обтекания потоком. Подставив (5) в (2) получим итоговое уравнение профиля оголовка (6):
Разработанный метод позволяет произвести профилирование быков водосливных сооружений и опор мостов. В большинстве конструкций принимается угол быка равный 90 градусов (
Компьютерное моделирование.
Для оценки влияния формы быка на пропускную способность сооружения с тремя различными конфигурациями криволинейных заострённых оголовков, было проведено компьютерное моделирование обтекания опоры в горизонтальном канале, состоящем из подводящего русла, двух отводных каналов и центральной разделительной опоры, выступающей в роли местного сопротивления. В работе исследуется наиболее неблагоприятный режим работы сооружения – формирование сверхкритического режима потока при обтекании опоры и подпора в верхнем бьефе сооружения. Такие условия могут формироваться в сооружениях на горных реках в условиях муссонного климата и высоких уклонах дна водотока. В этом случае, максимально проявляется разница в пропускной способности сооружения при различных очертаниях оголовков опор и быков.
Работы проводились в программном комплексе ANSYS 17.0. Компьютерное моделирование состояло из построения геометрической модели и расчетной сетки, определения начальных и граничных условий, а также выбора настроек решателя. Геометрическая модель канала, с установленными обтекаемыми опорами различных форм, выполнена в программе ANSYS DesighnModeler и представлена на рисунке 2. Геометрическая модель имела следующие размеры: ширина основного канала – 3 метра; ширина быка – 1 метр; ширина каждого из выходных каналов – 1 метр. Исследовалась пропускная способность сооружения с оголовком прямоугольной формы, а также оголовки криволинейного заостренного очертания построенные по форме дуги окружности и по принципу минимума кривизны.
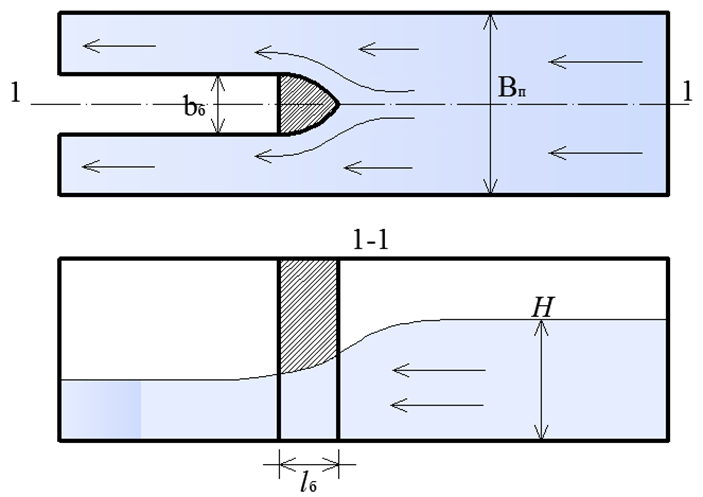
Рисунок 2. Схема исследуемой задачи обтекания опоры, где 
– ширина канала, , 
– глубина в верхнем бьефе канала (до сужения).
Построение сетки проводилось в программе ANSYS Meshing. В качестве вида сетки была выбрана трехмерная неструктурированная сетка с преимущественно четырехугольными ячейками. Максимальный линейный размер элемента расчетной сетки составил 0,1 метра для всех исследованных геометрических моделей. Для прямоугольного быка число элементов сетки составило 185110, число узлов 201006, для ячеек значения «скошенности» MOS=0,539 и «ортогональности» MOQ=0,99; для оголовка очерченного по дуге окружности число элементов сетки составило 271674, узлов 296976, MOS=0,168, MOQ=0,7141; по принципу минимума кривизны число элементов сетки 272283, узлов 297516, MOS=0,171, MOQ=0,705.
В качестве решателя была применена программа ANSYS Fluent. Основу расчета составляют уравнение неразрывности для несжимаемой жидкости и уравнение Рейнольдса. Для замыкания системы уравнений применена модель турбулентности k-
Realizable. Данная модель имеет такие преимущества [4, 5], как удовлетворение точным математическим ограничениям по напряжениям Рейнольдса, использование улучшенной формулы для определения турбулентной вязкости и использование уравнения диссипации, основанного на динамическом уравнении среднеквадратичных колебаний завихренности. Для моделирования течения потока со свободной поверхностью применен численный метод отслеживания объема жидкости в ячейке – VOF (volume of fluid). Данный метод позволяет рассматривать физическую задачу, как систему из двух несмешивающихся несжимаемых вязких сред [6]. Опыты проводились при объёмных расходах потока, лежащих в диапазоне от 1,5 до 6,75 м3/с, с равномерным интервалом варьирования 0,75 м3/с.
Результаты экспериментов
Для оценки влияния формы оголовков на изменение пропускной способности, в качестве искомой величины было выбрано значение коэффициента расхода сооружения, определяемое формулой (7):
где: 
– коэффициент расхода сооружения, 
– объёмный расход потока в канале.
Стенки канала и быка были приняты идеально гладкими и не оказывающими сопротивления движению потока. Поток в верхнем бьефе докритический, в нижнем бьефе – сверхкритический во всех опытах. Числа Фруда в подводящем канале лежат в диапазоне: 0,64-0,65 для прямоугольного быка, 0,7-0,73, для быка, очерченного по дуге круга, и для быка, построенного по принципу минимума кривизны. Для отводящих каналов число Фруда лежит в диапазоне: 1,2-1,72.
В результате анализа экспериментальных данных, представленных на рисунке 3, было определено, что коэффициент расхода сооружения при рассматриваемых расходах потока и отсутствии оголовка лежит в диапазоне 0,251-0,255; при использовании криволинейных заостренных оголовков обоих вариантов 0,27-0,28. Сравнение коэффициентов расхода делителя потока с оголовками криволинейного заостренного очертания показало, что пропускная способность сооружения немного меньше при использовании оголовков, построенных по дуге окружности, чем при построенном на основании принципа минимума кривизны. Процентное расхождение в коэффициенте расхода не превысило 0,27-1%, что лежит в пределах точности измерений и будет полностью компенсироваться потерями на трение, из-за разницы в смоченном периметре. Также стоит отметить, что моделирование производилось при достаточно высоких скоростях подвода потока. В реальных водосбросных сооружениях быки зачастую выдвинуты в верхний бьеф и скорости обтекания оголовков намного ниже, что уменьшает влияние формы быка на пропускную способность сооружения и делает предлагаемый метод профилирования ещё более выгодным.
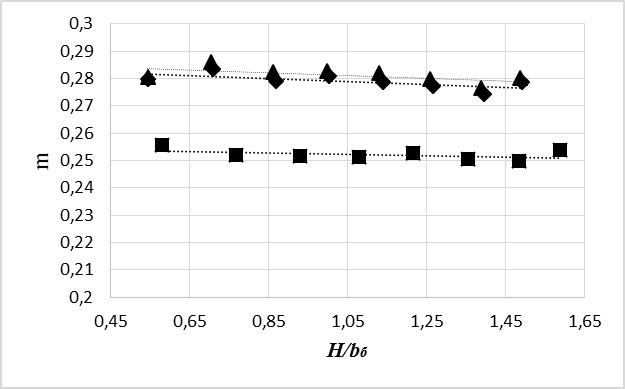
Рисунок 3. Результаты компьютерного эксперимента определения коэффициента пропускной способности делителя потока с различной формой входных оголовков, ▲ - результаты экспериментов для оголовка построенного по форме дуги окружности; ♦ - результаты экспериментов для оголовка, построенного по методу, основанному на принципе минимума кривизны; ■ - результаты экспериментов для прямоугольной опоры без оголовка.
Анализ результатов показывает, что использование вариационного принципа минимума кривизны даёт возможность выполнить более эффективное профилирование быков: уменьшить длину, смоченный периметр и объём затрачиваемых на строительство материалов без потерь пропускной способности сооружения.
Вывод.
В результате теоретического исследования на основе разработанной интерпретации вариационного принципа минимума кривизны получен теоретический метод профилирования криволинейных заостренных быков и оголовков опор, позволяющий уменьшить его размеры (длину, площадь и смоченный периметр) с сохранением прежней пропускной способности сооружения. При анализе исходного метода расчета обнаружена ошибочность распространенного утверждения, что при равных граничных условиях наименьшую длину и площадь имеет профиль, построенный по форме дуги окружности. Рассмотрение формулировки исходной вариационной изопериметрической задачи, показывает, что дуга кривой описывает профиль, имеющий наибольшую площадь, но не меньшую длину или кривизну поверхности. Применение профиля по принципу минимума кривизны вместо профиля, очерченного по дуге окружности, позволило уменьшить длину быка на 17,15%, площадь на 19,7%, смоченный периметр на 14,37%. Проведенное компьютерное моделирование задачи движения потока жидкости через делитель потока показало, что при обтекании быков потоком в докритическом состоянии, но достаточно близкому к бурному, коэффициент пропускной способности быка, построенного по принципу минимума кривизны, меньше на 0,27-1%, чем у быка очерченного по дуге окружности. Тем не менее, моделирование проводилось при использовании ряда допущений, реальная пропускная способность сооружения при использовании предлагаемого метода практически не изменяется.
1. Ибад-заде, Ю. А. Транспортирование воды в открытых каналах / Ю. А. Ибад-заде. - М.: Стройиздат, 1983. - 272 с.
2. Земляная Нина Викторовна, Шаланин Виктор Александрович Применение принципа минимума кривизны для расчета форм криволинейных водосливных поверхностей // Вестник ИШ ДВФУ. 2019. №4 (41).
3. Земляная Нина Викторовна, Шаланин Виктор Александрович Применение принципа минимума кривизны для расчета формы криволинейной водосливной поверхности низконапорных водосбросных сооружений // Вестник ИШ ДВФУ. 2018. №1 (34).
4. Коркодинов, Я. А. Обзор семейства K-ε моделей для моделирования турбулентности / Я. А. Коркодинов // Вестник ПНИПУ. Машиностроение, материаловедение. - 2013. - №2. - С. 5-16.
5. Shih, Tsan-Hsing & Liou, William & Shabbir, Aamir & Yang, Zhigang & Zhu, Jiang. (1995). A New κ-ε Eddy Viscosity Model for High Reynolds Number Turbulent Flows. Computers & Fluids. 24. 227-238.https://doi.org/10.1016/0045-7930(94)00032-T.
6. Копысов, С. П. Применение методов VOF и Sph для решения задач с развитой свободной поверхностью/ С. П. Копысов, Л. Е. Тонков, А. А. Чернова // Известия Института математики и информатики УдГУ. - 2015. - №2 (46) - 76-84.
